|
4. Расстояние, высота, давление, скорость, расчёт снижения
|
|
| Сварог | Дата: Четверг, 04.10.2012, 11:18 | Сообщение # 1 |
 Полковник
Группа: Пользователи
Сообщений: 167
Статус: Offline
| Чтобы рассчитать снижение, нужно иметь общее представление о перемещении летательного аппарата в воздушном пространстве и о величинах, с помощью которых измеряются его параметры.
Чтобы расширить представления (до объёмных), рассмотрим несколько важных тем, а уже исходя из них, будем выводить формулы для расчётов.
|
| |
| |
| Сварог | Дата: Четверг, 04.10.2012, 11:34 | Сообщение # 2 |
 Полковник
Группа: Пользователи
Сообщений: 167
Статус: Offline
| РАССТОЯНИЕ
Вообще говоря, по математическому определению, расстояние между двумя точками, это длина отрезка, их соединяющая. Когда мы смотрим на плоскую карту и видим два аэропорта, то, приложив линейку, мы можем узнать расстояние между ними. Это будет кратчайшее расстояние между двумя аэропортами или "расстояние по прямой".
Однако, если мы будем использовать это расстояние для наших расчётов, будь то расчёт начала снижения или расчёт топлива на рейс, то скорее всего мы попадём впросак. Всё потому, что как и автомобиль на земле, самолёт в небе движется по трассам, а они имеют далеко не прямолинейную форму.
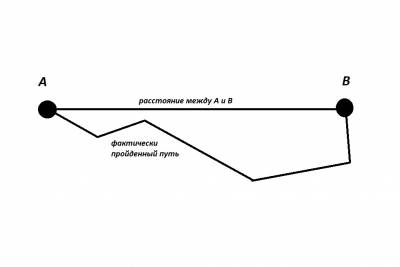
Как мы видим, фактически пройденное по трассам расстояние гораздо длиннее расстояния между аэропортами по прямой. Конечно, мы можем сесть на машину и ехать по прямой: по тротуарам, по клумбам, по газонам, поперёк дорог, пока не упрёмся в какое нибудь здание или сотрудника дорожной службы, если нам вообще повезет и в нас никто не въедет. Аналогично дело обстоит и с воздушным пространством.
Как нам узнать расстояние фактического пути (distance-to-go)?
Так как мы движемся по трассам, то есть от точки к точке, а на навигационных картах даны расстояния между точками, то, суммировав все длины отрезков пути, мы получим длину нашего пути.
Однако, это ещё не все нюансы. Всё было бы очень просто, если бы наш мир был плоским. Но он трёхмерен. А это подразумевает наличие высоты. До сего момента мы говорили не столько о фактическом пути самолёта, сколько об (ортогональной) проекции этого пути на плоскость абстрактной поверхности земли. Даже автомобиль, едущий по земле, проделывает путь не в плоскости, а в трёхмерном пространстве, так как едва ли мы найдём абсолютно ровную местность без перепада высот.
Посмотрим, каким теперь окажется наш путь.
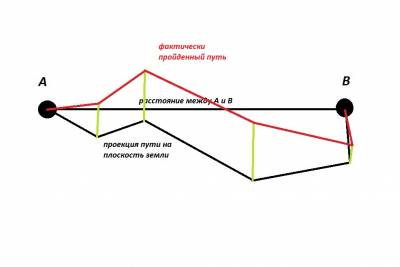
Заметьте, если мы двигаемся с постоянной высотой, то (пренебрегая кривизной поверхности земного "шара") можно сказать, что фактический путь (красная линия) ничем не отличается от его проекции на плоскость земли (черная линия), чего не скажешь о моментах изменения высоты. Здесь длина пути, проделанного между двумя точками будет длиннее кратчайшего расстояния между ними (того расстояния, которое мы бы прошли, двигаясь с постоянной высотой).
Что же вообще такое "точка", от которой или к которой движется наш самолёт? Вот две точки А и В, которые мы можем видеть на плоской карте:
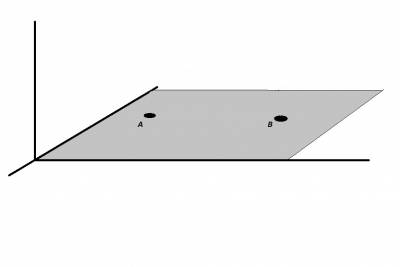
Каждая точка - это либо какая-то передающая навигационная станция на земле (VOR, NDB...) или это просто абстрактная пара координат абстрактной плоскости поверхности земли, не имеющая под собой физической основы. Но это сути не меняет, так как в любом случае эта точка фиксирована на данной плоскости (карте).
Однако, наш самолёт движется не в плоскости, а в трёхмерном пространстве и любую точку он может пройти на разных высотах. И если наш самолёт пройдёт точку А на одной высоте, а точку В на другой, то есть, путь между точками не будет параллельным "плоскости земли", то для нас, находящихся в самолёте, расстояние между этими точками окажется бОльшим, нежели оно есть по прямой на плоскости.

Фактически, для нас точка перестаёт быть "точкой", и превращается в перпендикуляр с началом в фиксированной точке на плоскости (карте). И мы видим, насколько может измениться расстояние, проходимое между этими точками, в зависимости от траектории движения.
В самолётах с бортовыми компьютерами всю вычислительную работу выполняет компьютер. Нам же пришлось бы сидеть с карандашом и справочником по геометрии, если бы не одна очень удобная величина - путевая скорость (Ground Speed), рассчитываемая компьютером или приёмником GPS, и позволяющая пренебречь вертикальным профилем нашего пути в плане учёта расстояния, возвращая нас к удобочитаемым плоским картам. Но об этом чуть позже.
|
| |
| |
| Сварог | Дата: Четверг, 04.10.2012, 12:45 | Сообщение # 3 |
 Полковник
Группа: Пользователи
Сообщений: 167
Статус: Offline
| ВЫСОТА И ДАВЛЕНИЕ
Я никогда не задумывался о понятии высоты до того, как стал интересоваться авиацией. Высота в 5 метров всегда была для меня высотой в 5 метров, а самолёт летящий на высоте 10 километров, просто летел на высоте 10 километров.
Ну и что здесь такого? Выдал какую-то тавтологию... Однако нет. Потому что высота - это тоже расстояние, а расстояние измеряется между двумя точками. Так от какой точки или уровня измерять высоту? Казалось бы логично заявить - от уровня земли. И всё было бы так, имей земля плоскую форму поверхности. Однако, она имеет рельеф, с большими перепадами высот. И показания высот могли бы каждые 5 секунд колебаться с большой амплитудой, делая показания высоты бесполезными. Поэтому нам нужно ввести некий эталон, точку отсчёта, которая бы не зависела ни от чего иного. В качестве такого эталона взят уровень моря.
В России высоты точек земной поверхности над уровнем моря отсчитывают от среднемноголетнего уровня Балтийского моря, определённого от нуля Кронштадтского футштока. Это абсолютная высота. С её помощью измеряются превышения аэропортов (высоты, на которых находится местность аэропортов), эшелоны, на которых летят самолёты.
Кроме понятия абсолютной высоты, есть ещё понятие относительной высоты. Относительная высота - это превышение какой-либо точки земной поверхности относительно другой точки, равное разности абсолютных высот этих точек (например, высота горной вершины над уровнем дна ближайшей долины или высота, на которой находится самолёт относительно порога ВПП, на которую планируется приземлиться).
Но для некоторых случаев, бывает удобнее другая высота. Истинная высота. То есть высота от поверхности земли над тем участком, над которым пролетает самолёт. Она для нас необходима на посадке, хотя можно выполнять посадку используя показания абсолютной высоты, при условии, что мы точно знаем высоту превышения торца полосы, на которую планируем приземлиться. Высоту от земной поверхности измеряет радиовысотомер. Дальность его действия обычно ограничена 2500 футов (760 метров).
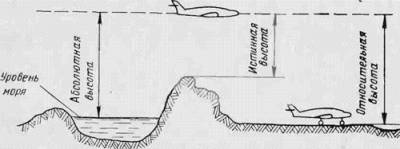
Как мы видим, положение самолёта может характеризовать три разные высоты: относительно уровня моря, над пиком скалы, который он пролетает в данный момент и относительно уровня порога ВПП, на которую планируется произвести посадку.
Понятно, что истинная высота в точке, над которой находится самолёт и относительная высота (относительно уровня этой точки) - совпадают.
Но вернёмся к барометрическому высотомеру и некоторым особенностям его работы. Само название "барометрический" подсказывает нам, что принцип его деятельности связан с атмосферным давлением. Давление в атмосфере изменяется с изменением высоты, поэтому, измеряя фактическое давление и высчитывая разницу с установленным, высотомер показывает нам высоту, на которой он находится.
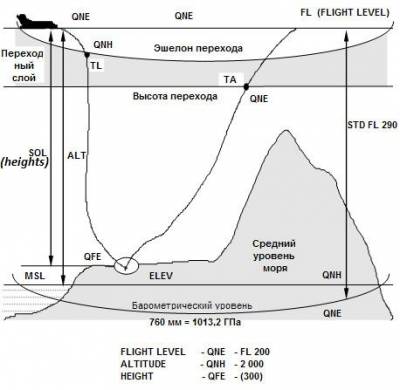
Давление на эталонном уровне моря QNE (Q-code Nautical Elevation) или стандартное атмосферное давление на уровне моря составляет 1013,2 гПа или 760 мм рт. ст. или 29,92 дюйма рт. ст.
По идее, выставив на высотомере значение QNE (стандартного атмосферного давления), мы могли бы узнать высоту превышения аэропорта, на стоянке которого мы находимся или высоту, на которой мы летим....если бы не одно но. В зависимости от погодных условий, на одной и той же высоте данной местности давление может колебаться, и если значение давления на высотомере не будет совпадать с фактическим атмосферным давлением в данной местности, то и показания высоты будут неправильными.
Чтобы учесть и скорректировать данный факт, используется QNH (Q-code Nautical Height) - атмосферное давление в данной точке, приведенное к среднему уровню моря (MSL). При установленном QNH высотомер показывает высоту относительно среднего уровня моря (при стандартной температуре). Значение приведённого давления нам говорит диспетчер, сводка МЕТАР или сообщение ATIS. И суть его заключается в том, чтобы учесть врЕменные отклонения фактического давления атмосферы в зоне аэропорта, дабы высотомер показывал высоту относительно уровня моря. Понятно, что на земле он будет показывать высоту превышения аэропорта или той точки аэропорта, на которой вы находитесь, если аэропорт имеет значительный разброс высот.
Таким образом, перед взлётом или после приземления, наш высотомер должен показывать, вообще говоря, не нулевое значение, а высоту превышения аэропорта.
В некоторых регионах (например, в России) используется не приведённое давление, а так называемое QFE ( Q-code Field Elevation ) - атмосферное давление аэродрома на уровне порога ВПП. И выставив его на высотомере, мы получим относительную высоту. А находясь перед взлётом на самом пороге ВПП, наш высотомер покажет нулевое значение, и все дальнейшие показания высоты будут производиться относительно этого уровня.
Но не все самолёты (особенно зарубежных производителей, например, Боинг) сертифицированы для использования QFE. Вообще говоря, если на самолёте не установлено специальное оборудование, то использовать высотомер с выставленным давлением QFE запрещено РЛЭ (руководством лётной эксплуатации). Вместо этого подобные типы самолётов оборудованы радиовысотомером, который показывает высоту от уровня той точки, над которой находится самолёт. И точность радиовысотомера очень велика. Принцип деятельности радиовысотомера заключается в испускании и улавливании луча, отраженного от поверхности земли и расчёте расстояния, исходя из постоянной скорости луча и времени между выходом луча и его возвратом. Но на больших скоростях и больших высотах этот принцип становится бесполезным, так как за то время, за которое луч пройдет свой путь от передатчика до поверхности земли и обратно, самолёт успеет сместиться на довольно большое расстояние и окажется над точкой, до которой будет совершенно иное расстояние.
Так как на всей протяжённости пути давление то и дело будет меняться, то пилоты просто замучаются выставлять новые значения давления, да и откуда они их будут брать? Для такого случая существует понятие высоты перехода, которую дают по давлению QNH или QFE. Набрав эту высоту мы выставляем на высотомере значение стандартного давления QNE, равное 1013,2 гПа или 760 мм рт. ст. или 29,92 дюйма рт. ст. И на протяженности всего полёта мы будет отмерять высоту по этому давлению до тех пор, как диспетчер скажет нам его сменить.
Понятно, что на всем пути фактическое давление едва ли будет постоянным и равным стандартному. А значит, разные самолёты, находящиеся в зонах с разным давлением на одной высоте по показаниям высотомера, фактически будут находиться на разных высотах. Но при приближении и вхождении в зону одного давления их высоты "согласуются".
Ну и на снижении, на эшелоне перехода, нас проинструктируют к смене давления на высотомере. Это будет уже либо QNH либо QFE в зависимости от региона и типа самолёта. Таблицы соответствия высот по QNH и QFE приводятся в схемах аэропортов, в которых используется QFE (например, аэропорта Шереметьево).
В английском эквиваленте используются следующие термины:
ALTITUDE (A)- высота относительно уровня моря (QNH).
HEIGHTS (H) - высота относительно уровня земли (QFE, радиовысотомер).
FLIGHT LEVEL (FL) - эшелон (QNE).
TRANSITION ALTITUDE (TA) - высота перехода (переходим на QNE).
TRANSITION LEVEL (TL) - эшелон перехода (переходим на QNH или QFE).
А вот некоторые картинки, демонстрирующие выше сказанное:

А вот, что может случиться, если забыть перевести давление на эшелоне перехода со стандартного (QNE) на приведённое давление (QNH), которое присутствует в данное время в данной местности:
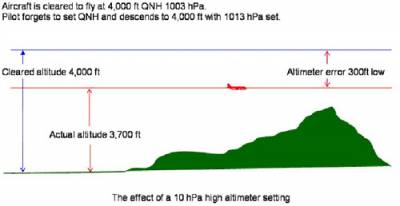
То есть борту было предписано снижаться на высоту 4000 футов по приведённому давлению 1003 гектопаскаля, но пилот по какой-то причине не установил это давление на высотомере и снизился на высоту 4000 футов по стандартному давлению 1013,2 гектопаскаля, в результате чего оказался ниже на 300 футов (90 метров), после чего их долго искали в районе горы Монглотомбо.
И ещё раз, обратите внимание на разницу высоты по давлению QFE и по радиовысотомеру. По QFE вам дадут высоту относительно уровня (превышения) небольшого "пятачка" местности, как порог ВПП, и где бы вы ни находились, ваша высота будет измеряться относительно этого уровня. Если вы идёте в постоянном снижении, то эта высота будет постоянно строго уменьшаться. Высотомер же вам даёт значение фактической высоты от той точки, над которой вы находитесь в данный момент. И если вы идёте в постоянном снижении, а местность очень неоднородна, то возможен и такой случай, что после высоты в 500 футов, по радиовысотомеру, вы получите высоту в 1000 футов, например, пролетая над оврагом.
|
| |
| |
| Сварог | Дата: Четверг, 04.10.2012, 14:19 | Сообщение # 4 |
 Полковник
Группа: Пользователи
Сообщений: 167
Статус: Offline
| СКОРОСТЬ
Казалось бы, ну о чём тут говорить? Сидишь себе за рулём роскошного авто, жмёшь на педальку газа и поглядываешь, чтобы стрелка спидометра не зашкалила за допустимое значение, предписанное только что промелькнувшим дорожным знаком, особенно, когда за следующим поворотом частенько греют местечко голодные сотрудники дорожной службы обеспечения безопасного и комфортного автомобильного движения. А вот в небе ну всё не как ... на земле.
Итак, что такое скорость? В отличие от понятия "времени" (которое на самом деле является иллюзорным понятием, существующим только в психике, вопреки яростно внедряемого в умы общественности стереотипа), в основе которого лежит всё то же движение с постоянной скоростью, скорость - это вполне действительная характеристика вселенских процессов, в том числе и в авиационной отрасли.
Суть скорости в "быстроте" (воспринимаемой ощущениями) изменения чего бы то ни было. В данном случае, это изменение положения некой точки относительно абстрактной системы координат, или проще говоря, относительно другой точки. Если бы мы двигались (не важно, как быстро, не важно с каким ускорением) в однородном пространстве и не испытывали при этом никаких ощущений силовых воздействий в сознании, то понятие скорости просто потеряло бы для нас смысл.
Однако в физическом слое Вселенной мы имеем полный спектр подобных ощущений, а вместе с ними и поведения материальной точки (в данном случае нашего самолёта), поэтому для начала постараемся перечислить все различные вариации скоростей, встречающиеся в авиации.
Итак, с какими разновидностями скоростей мы встретимся в авиации - что мы можем найти в справочниках интернета:
Воздушная скорость - скорость ЛА относительно воздуха. Различают два вида воздушной скорости:
истинная воздушная скорость (TAS) - действительная скорость, с которой ЛА движется относительно окружающего воздуха за счёт силы тяги двигателя(ей), вектор скорости в общем случае не совпадает с продольной осью ЛА, так как на его отклонение влияют угол атаки и скольжение ЛА; и приборная воздушная скорость (IAS) - скорость, которую показывает прибор, измеряющий воздушную скорость. На любой высоте эта величина однозначно характеризует несущие (аэродинамические) свойства планера в данный момент. Значение приборной скорости используется при пилотировании ЛА.
Путевая скорость (GS) или скорость ЛА относительно земли. Зависит от воздушной скорости, скорости и направления ветра. Значение рассчитывается или измеряется при помощи технических средств самолётовождения. Используется при решении навигационных задач.
Крейсерская скорость - воздушная скорость горизонтального полета, при которой величина отношения потребной тяги к скорости полета минимальна. На крейсерской скорости военная авиация совершает обычно свои боевые действия, а гражданская - рейсы по маршрутам, трассам. Скорость крейсерская составляет 0,7-0,8 максимальной скорости полета.
Число́ Ма́ха — в механике сплошных сред — отношение локальной скорости потока к местной скорости звука. Зачастую используется упрощённое определение числа Маха как отношения скорости тела, движущегося в газовой среде, к скорости звука в данной среде. Такое определение не вполне корректно, так как скорости потоков в окрестностях движущегося тела зависят от его формы.
Чаще всего такое определение используется в оценочных характеристиках ЛА: их скорость задаётся безразмерным числом в формате "M n ", где "n "-десятичное число. Например, "скорость M 2 " — обозначает что скорость летательного аппарата в 2 раза превышает скорость звука. Пересчёт такой скорости в линейную скорость затруднён, так как скорость звука в воздухе зависит от его плотности (и, соответственно, высоты полёта) и температуры. Вместе с тем шкала скоростей Маха широко применяется в авиации, так как аэродинамические свойства и условия обтекания летательных аппаратов при близких значениях числа Маха также близки.
Скорость сваливания - минимальная приборная скорость (с внесенными аэродинамической и инструментальной поправками), при которой самолет управляем в заданных условиях.
V1 - скорость принятия решения. Это расчитанная для данных условий взлета скорость, до достижения которой должно быть принято решение о продолжении или прекращении взлета. Причем оставшейся располагаемой дистанции должно хватать как для прерванного, так и для продолженного взлета (даже с учетом потери тяги отказавшего двигателя, если таковое произошло). В дистанцию продолженного взлета входит остаток ВПП, а в дистанцию прерванного взлета - остаток ВПП + КПБ.
V1 зависит от многих факторов, таких, как: метеоусловия (ветер, температура), состояние покрытия ВПП, взлетный вес самолёта и другие. В случае, если отказ произошёл на скорости, большей V1, единственным решением будет продолжить взлёт и, затем произвести посадку. Большинство типов самолётов ГА сконструированы так, что, даже если на взлёте откажет один из двигателей, остальных двигателей хватит, чтобы, разогнав машину до безопасной скорости, подняться на минимальную высоту, с которой можно зайти на глиссаду и посадить самолёт.
Vr - скорость начала подъёма передней опоры шасси.
V2 - безопасная скорость для взлёта.
Vref - расчетная скорость посадки.
VMO - Vmaximum operating - максимальная эксплуатационная скорость.
Вертикальная скорость - изменение высоты полёта за единицу времени. Равна вертикальной составляющей скорости ЛА.
Скорость ветра - скорость горизонтального перемещения воздуха относительно земной поверхности. Скорость ветра обычно определяется в метрах в секунду, узлах и километрах в час.
|
| |
| |
| Сварог | Дата: Пятница, 05.10.2012, 12:23 | Сообщение # 5 |
 Полковник
Группа: Пользователи
Сообщений: 167
Статус: Offline
| Рассмотрим, как летит самолёт в воздушном пространстве:
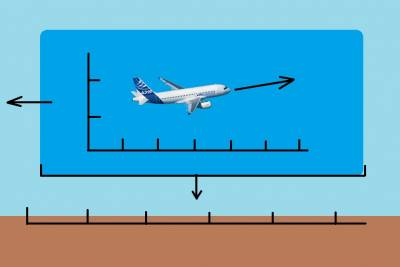
Для человека, стоящего на земле, самолёт воспринимается как просто летящий в небе и перемещающийся относительно земли объект.
Но на самом деле всё немного сложнее. Самолёт летит в некой воздушной массе и перемещается относительно неё. Если мы будем рассматривать воздушную массу как фиксированную и введём в ней абстрактную систему координат, то самолёт будет перемещаться относительно этой системы координат с некоторой скоростью, называемой истинной воздушной скоростью (TAS - true air speed). При этом воздух будет обдувать крыло, создавая определенной давление на него, что собственно и порождает подъёмную силу. Это приборная воздушная скорость (IAS - indocared air speed) - та скорость, которую мы видим на показателе скорости и она скорее характеризует силу давления воздуха на крыло. А именно от этой силы и зависят аэродинамические свойства самолёта, в частности, подъёмная сила крыла. Казалось бы, истинная и приборная скорости - это одно и тоже. Но не совсем. У земли TAS=IAS, но чем выше, тем разреженней воздух, тем меньше давление он оказывает на крыло, а так же меньше и лобовое сопротивление. В итоге на одной и той же силе тяги с большей высотой самолёт разгоняется быстрее (ведь лобовое сопротивление становится меньше), но при этом ему и нужно лететь быстрее (TAS), чтобы поддерживать необходимое давление набегающего воздушного потока (IAS), чтобы поддерживать необходимую подъёмную силу крыла. Выходит, если поддерживать IAS постоянной, то при увеличении высоты, TAS будет увеличиваться. Вектор истинной воздушной скорости направлен туда, куда движется самолёт, будь то параллельно земле или под углом к поверхности земли.
Таким образом, самолёт движется относительно воздушной массы с определенной скоростью (TAS). Допустим, самолёт движется параллельно земле (не меняя высоту), а воздушная масса неподвижна относительно земной поверхности. Рассмотрим перпендикулярную проекцию самолёта на плоскость абстрактной земной поверхности.
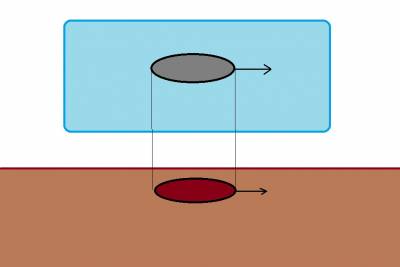
Проекция будет двигаться вместе с самолётом, причём с такой же скоростью. Скорость перемещения проекции - это и есть путевая скорость или скорость самолёта относительно земли (GS - ground speed) и в этом случае GS=TAS.
Теперь рассмотрим случай, когда самолёт движется под углом к плоскости земной поверхности, например, набирает высоту:
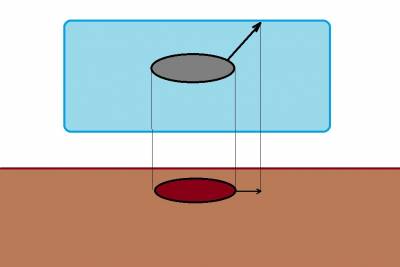
Допустим, наш самолёт относительно воздуха движется с той же скоростью TAS, причём теперь вектор этой скорости направлен под углом к плоскости земли. Рассмотрим же проекцию ("тень самолёта"). Вектор скорости перемещения проекции по прежнему направлен в ту же сторону, однако его величина, как мы видим (то есть величина проекции вектора скорости), уменьшилась. А для нас это означает, что путевая скорость, то есть скорость перемещения относительно земли (Ground Speed) стала меньше. Вообще говоря, зная угол, под которым перемещается самолёт (НЕ тангаж!!!) с помощью простых тригонометрических функций можно самому высчитать Ground Speed. Если бы наш самолёт полетел перпендикулярно вверх, то его путевая скорость стала бы равной нулю.
Но обычно такого идеального состояния не бывает, потому что кроме всего прочего ещё дует ветер. То есть воздушный слой перемещается относительно земли:
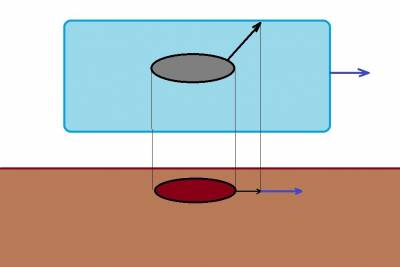
То есть теперь к путевой скорости добавилась величина в данном случае попутного ветра, GS=TAS+W, где W - это значение составляющей скорости ветра. Почему составляющей? Потому что ветер может дуть и вбок, нам же нужна та составляющая скорости ветра, которая совпадает с нашим курсом движения (ну или обратно направлена, если ветер встречный). Составляющую ветра так же можно посчитать с помощью простых тригонометрических функций.
Ну а вообще говоря, за нас все эти рутинные расчёты выполняет бортовой компьютер или приёмник GPS.
А вот демонстрация скоростей на примере пикирования боинга 737:

Теперь мы вплотную подошли к расчёту точки начала снижения.
|
| |
| |
| Сварог | Дата: Пятница, 05.10.2012, 13:42 | Сообщение # 6 |
 Полковник
Группа: Пользователи
Сообщений: 167
Статус: Offline
| РАСЧЁТ ТОЧКИ НАЧАЛА СНИЖЕНИЯ
Будем рассчитывать бесступенчатое снижение с высоты эшелона до необходимой высоты, например, высоты входа в глиссаду. Если на пути есть промежуточные горизонтальные отрезки, то их длины нужно будет прибавить к общему значению, а снижение рассчитывать для каждого участка изменения высоты. Так же необходимо будет учесть отрезки пути, необходимые для замедления скорости самолёта, ибо на этих участках скорость снижения может уменьшаться вплоть до нулевого значения.
Сразу скажу, что точное значение мы не сможем посчитать, иначе нам нужно будет знать скорость и направление ветра в каждой точке нашего пути и вычислять интегралы вместо того, чтобы управлять самолётом.
Итак, допустим, мы находимся на высоте H1 (футов) и нам нужно спуститься до высоты H2 (футов), причём, на этой высоте нам нужно быть в точке Х. Вопрос: на каком удалении L от точки Х нужно начать снижение?
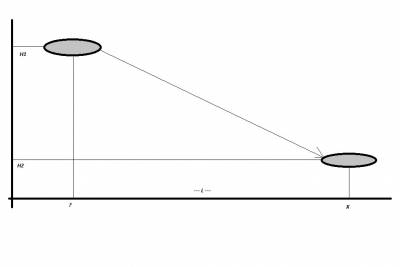
Прежде всего, для нас играет роль не столько исходная и конечная высота, сколько значение её изменения ∆H=H1-H2. Дальше воспользуемся простой формулой зависимости скорости и расстояния, считая, что путевая скорость измеряется в узлах (морская миля-в-час), вертикальная скорость в футах-в-минуту, а высота в футах: L=tV.
Так как снижение и перемещение от точки начала снижения до нужной точки пути произойдёт за одно и то же время, получим равенство:
L/GS=∆H/60 VS, где GS - ground speed (путевая скорость), а VS - vertical speed (вертикальная скорость). Так как время с обоих сторон должно измеряться в одинаковых единицах, например, часах, а скорость снижения дана нам в футах-в-минуту, то приводим к однородности величин, разделив время снижения на 60.
Откуда получим формулу: L=∆H GS/60 VS.
Далее формулу нужно адаптировать для каждого типа самолётов, так как разные самолёты имеют разный профиль снижения. Ну и нужно не забывать, что на высоте 10000 футов, нам нужно будет снизить скорость до 250-240 узлов. Поэтому получим две составные части снижения: с эшелона до 10000 и с 10000 до требуемой высоты.
И осталось разобраться с путевой скоростью, которая напрямую зависит от истинной воздушной скорости. А, как мы знаем, с уменьшением высоты, истинная воздушная скорость будет уменьшаться (при постоянной приборной), стремясь своим значением к приборной скорости. Всё, что мы можем здесь сделать - это сложить два крайних значения и разделить пополам, получив среднее значение путевой скорости GS'=(GS1+GS2)/2.
Тогда наша формула примет вид: L=[(H1-10000) GS1' ]/ 60 VS1+[(10000-H2) GS2']/ 60 VS2.
Не только путевая скорость уменьшится, но и вертикальная. Чем медленнее летит самолёт, тем с меньшей вертикальной скоростью ему нужно будет снижаться, и наоборот.
Но так же не забываем про дистанцию, необходимую для торможения, перед высотой 10000 футов до скорости 240-250 узлов, и перед заходом на посадку до посадочной скорости, во время которого самолёт может практически прекращать снижение.
Исходя из всего этого получим расчётную формулу:
L=[(H1-10000) GS1' ]/ 60 VS1+[(10000-H2) GS2']/ 60 VS2+∆L
где H1 - высота эшелона, H2 - конечная высота снижения, GS1', GS2'- средняя путевая скорость на 1 2 втором участке снижения, VS1', VS2' - вертикальная скорость на 1 и 2 участках снижения, ∆L - запас пути для замедления путевой скорости и запас на непредвиденный случай.
Например, для Боинга-737, в условиях безветрия стандартное снижение будет таким.
С эшелона FL340 до 10000 футов: приборная скорость 280, путевая скорость на эшелоне ~450 узлов, вертикальная скорость ~2200 футов-в-минуту, путевая скорость на высоте 10000 футов ~250 узлов.
Ниже 10000 футов до входа в глиссаду на 1600 футах: приборная скорость 240 узлов, путевая скорость от 250 до 150 узлов, вертикальная скорость ~ 1400 футов-в-минуту.
Запас на торможение 10 миль.
В безветренную погоду мы получим следующее удаление точки начала снижения.
L= 24000x350/60x2200+8400x200/60x1400+10~=95 миль. Накинув ещё 5 миль на всякий случай, получим 100 миль. То есть за 100 миль от точки Х (не по прямой, а distance-to-go!!!) мы начинаем стандартное снижение с двумя участками замедления: перед 10000 футов и на последнем участке, когда будем конфигурировать самолёт для посадки.
Конечно, это неточные расчёты, но для точных расчётов нам понадобилась бы масса параметров и громоздкие формулы. Ну а чтобы полностью избавить себя от подобного бремени, мы можем просто переложить это действие на бортовой компьютер, в котором должен быть правильно введён маршрут и по возможности вписаны ветра на различных эшелонах (в симуляторе нам это едва ли удастся сделать, так как просто неоткуда брать подобные значения).
|
| |
| |
| Сварог | Дата: Пятница, 05.10.2012, 16:31 | Сообщение # 7 |
 Полковник
Группа: Пользователи
Сообщений: 167
Статус: Offline
| Некоторые источники предлагают нам ещё более простой способ расчёта начала снижения.
Начинать снижение нужно на удалении в три раза превышающем высоту эшелона (в тысячах футов), и снижаться с вертикальной скоростью (в футах-в-минуту), равной пятикратной путевой скорости (в узлах).
L= 3 ∆H /1000. VS= 5 GS.
Например, с высоты 35000 футов нам нужно начать снижение на удалении 105 миль и снижаться с вертикальной скоростью в 5 раз превышающей значение путевой скорости, например, для 450 узлов это будет 2250 футов-в-минуту, для 240 узлов - 1200 футов-в-минуту.
|
| |
| |
| Сварог | Дата: Пятница, 05.10.2012, 16:34 | Сообщение # 8 |
 Полковник
Группа: Пользователи
Сообщений: 167
Статус: Offline
| Для глиссады с углом наклона в 3 градуса, точку входа в глиссаду можно рассчитать так:
H=315 L, где H - высота в футах, L - удаление от торца ВПП в милях.
|
| |
| |



















